The air crackles with a nervous energy. You stare at the carefully printed pages in front of you, each question a potential hurdle on the path to your AP Calculus AB score. The 2018 International Practice Exam looms, a formidable opponent demanding your best. But fear not, aspiring mathematicians! This comprehensive guide delves into the 2018 International Practice Exam, dissecting its complexities and equipping you with the tools to conquer its formidable challenges. We’ll examine the intricacies of each Free Response Question (FRQ), providing insights and strategies to maximize your score. Prepare to unlock the secrets of calculus and solidify your understanding of this pivotal subject.
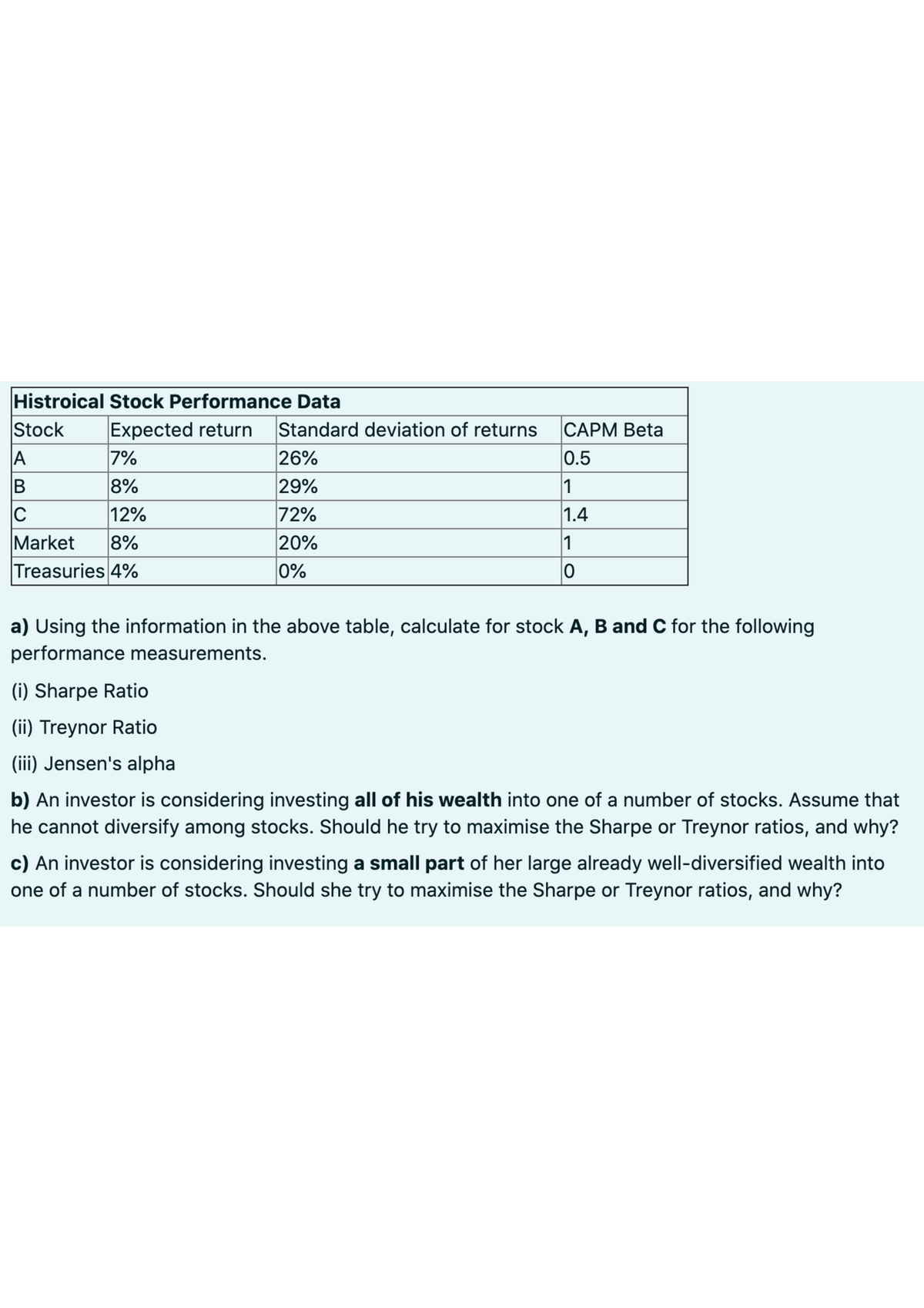
Image: www.studocu.com
The 2018 International Practice Exam is a valuable resource for any student preparing for the AP Calculus AB exam. Composed of six challenging FRQs, it mirrors the actual exam format, offering a realistic simulation of the testing experience. This exam is designed to assess your ability to apply calculus concepts in a variety of contexts, pushing you to think critically and demonstrate your mastery of the subject. Each FRQ presents a unique problem-solving scenario, requiring you to navigate intricate equations, analyze graphs, and interpret real-world applications.
Delving Deeper into the 2018 International Practice Exam
Let’s dive into the depths of the 2018 International Practice Exam, exploring each FRQ and uncovering the strategies needed to excel.
FRQ 1: Functions and Their Derivatives
This FRQ explores the relationship between a function and its derivative. You’ll analyze a given function, determine its derivatives, and interpret their meaning in the context of the problem. For example, you might be asked to find the critical points of a function, analyze its intervals of increase and decrease, or determine the concavity of its graph.
Key Strategies:
- Understanding Derivatives: Master the rules of differentiation, including the power rule, product rule, quotient rule, and chain rule.
- Applying the First and Second Derivative Tests: Utilize these tests to identify critical points, analyze intervals of increase and decrease, and determine concavity.
- Interpreting Context: Remember that calculus is not just about manipulating equations. Connect your findings to the real-world context of the problem.
FRQ 2: Areas and Volumes
This FRQ focuses on calculating areas and volumes using definite integrals. You’ll be given a region bounded by curves and asked to find its area or the volume of a solid generated by rotating that region.
Key Strategies:
- Fundamental Theorem of Calculus: Apply this theorem to calculate definite integrals and find areas and volumes.
- Understanding Geometric Shapes: Recognize common shapes like circles, squares, and triangles and their corresponding formulas.
- Choosing the Right Method: Determine whether to use the disk, washer, or shell method based on the solid’s geometry and rotation axis.
FRQ 3: Related Rates
This FRQ introduces the concept of related rates, examining how rates of change of different quantities are related. You’ll be given a scenario involving changing variables and asked to find the rate of change of one quantity in terms of the rate of change of another.
Key Strategies:
- Setting up Equations: Establish relationships between the variables involved in the problem.
- Implicit Differentiation: Differentiate both sides of the equation with respect to time, treating variables as functions of time.
- Substituting Values: Use the given rate of change to find the unknown rate of change.
FRQ 4: Differential Equations
This FRQ introduces differential equations, equations that involve derivatives. You might be asked to solve a differential equation, find a particular solution, or interpret its solution in the context of a real-world situation.
Key Strategies:
- Recognizing Types of Differential Equations: Identify the type of differential equation to determine the best solution technique (e.g., separation of variables, integrating factors).
- Solving Initial Value Problems: Use an initial condition to find the specific solution to a differential equation.
- Interpreting Solutions: Identify the meaning of the solution within the context of the problem.
FRQ 5: Applications of Calculus
This FRQ presents a real-world scenario where calculus can be applied to solve a practical problem. You’ll need to use your understanding of various calculus concepts to analyze the situation, formulate a solution, and interpret your findings.
Key Strategies:
- Translating Words into Math: Convert the problem’s verbal description into mathematical equations and relationships.
- Applying Calculus Concepts: Use appropriate calculus techniques (e.g., optimization, related rates, differential equations) to address the problem.
- Communicating Your Findings: Clearly explain your solution and its implications in the context of the problem.
FRQ 6: Finding a Function
This FRQ presents information about a function and asks you to determine its formula. This could involve using derivatives, integrals, or a combination of both.
Key Strategies:
- Identifying Key Characteristics: Analyze the given information (e.g., derivatives, intercepts, asymptotes) to build a picture of the function’s behavior.
- Using Derivatives and Integrals: Employ differentiation and integration to reverse-engineer the function from its given attributes.
- Testing Your Solution: Ensure your function satisfies all the given conditions.
Expert Insights: A Path to Success
As you navigate the challenges of the 2018 International Practice Exam, remember these valuable insights from experienced educators and AP Calculus veterans:
- Practice, Practice, Practice: The key to success lies in consistent practice. Work through as many FRQs as possible, analyzing your strengths and weaknesses. Utilize online resources, textbooks, and practice exams to sharpen your skills.
- Master the Fundamentals: Ensure a strong foundation in fundamental calculus concepts like limits, derivatives, integrals, and applications. Review foundational topics as needed.
- Understand the Exam Expectations: Familiarize yourself with the scoring guidelines and the expectations for each FRQ. Understand how your responses will be evaluated.
- Seek Guidance and Collaboration: Don’t hesitate to collaborate with classmates, study groups, or teachers. Discussing challenging concepts and sharing solutions can illuminate new perspectives.
Actionable Tips for Maximizing Your Score:
- Time Management: Allocate roughly 15 minutes per FRQ, leaving a few minutes at the end to review your work.
- Show Your Work: Demonstrate your steps clearly and concisely, even if you’re unsure about the final answer. Partial credit is awarded for correct work.
- Use Proper Notation: Adhere to mathematical conventions for notation, variables, and symbols.
- Communicate Effectively: Write your answers in complete sentences, explaining your reasoning and connecting your findings to the problem’s context.

Image: deborahsilvermusic.com
2018 International Practice Exam Ab Frq
A Journey Towards Mastery
The 2018 International Practice Exam is a powerful tool for your AP Calculus AB journey. By understanding its structure, mastering its concepts, and implementing the strategies outlined above, you can confidently tackle this challenging exam and achieve a score that reflects your hard work and dedication. Remember, the path to mastery is paved with practice, perseverance, and a deep understanding of the powerful tools of calculus.





