Have you ever stared at a triangle on a worksheet, feeling overwhelmed by the jumble of angles and sides? You’re not alone! Trigonometry, the study of triangles, can feel like a maze of calculations and formulas. But fear not! This article will empower you with the knowledge you need to navigate the world of missing sides and angles with confidence. We’ll embark on a journey through the fascinating realm of trigonometry, equipping you with the tools to master those seemingly daunting worksheets.
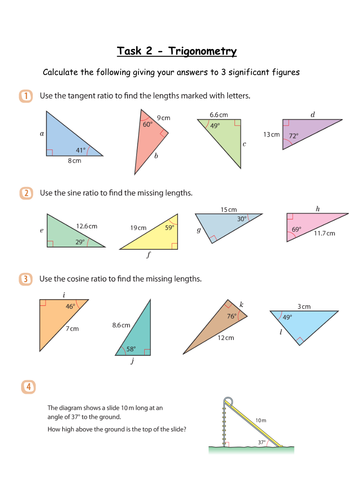
Image: worksheetpic101.s3.amazonaws.com
Imagine yourself standing at the base of a towering mountain, its peak shrouded in mist. You want to know its height, but reaching the summit seems impossible. This is where trigonometry comes to the rescue. Using angles, sides, and a bit of clever math, you can calculate the mountain’s height from your vantage point. Trigonometry isn’t just about mountains; it’s about understanding relationships between angles and sides within any triangle, which has vast applications in fields like engineering, architecture, and even navigation. Let’s dive into the world of triangles and unlock the secrets of those missing sides and angles!
Trigonometric Ratios: The Cornerstone of Finding Missing Values
The heart of trigonometry lies in understanding the relationships between the sides of a right triangle relative to its acute angles. These relationships are defined by three primary trigonometric ratios: sine (sin), cosine (cos), and tangent (tan). Each ratio represents a specific ratio of sides, providing a key to unlocking missing side lengths or angle measures.
- Sine (sin): This ratio represents the opposite side to an angle divided by the hypotenuse (the longest side in a right triangle). Sin(angle) = Opposite / Hypotenuse.
- Cosine (cos): This ratio represents the adjacent side to an angle divided by the hypotenuse. Cos(angle) = Adjacent / Hypotenuse.
- Tangent (tan): This ratio represents the opposite side to an angle divided by the adjacent side. Tan(angle) = Opposite / Adjacent.
Visualizing these ratios can be helpful. Imagine a right triangle with an acute angle labeled ‘A.’ The side opposite angle A is labeled ‘o,’ the side adjacent to angle A is labeled ‘a,’ and the hypotenuse is labeled ‘h.’ The trigonometric ratios for angle A would be:
- sin(A) = o/h
- cos(A) = a/h
- tan(A) = o/a
Mastering the Art of SO-CAH-TOA
Remember those trigonometric ratios? They’re the foundation for solving problems involving missing sides and angles. To make them easier to recall, you can use the nifty mnemonic “SOH-CAH-TOA.”
- SOH: Sine = Opposite / Hypotenuse
- CAH: Cosine = Adjacent / Hypotenuse
- TOA: Tangent = Opposite / Adjacent
This acronym acts as a handy reminder of the way these ratios relate to side lengths in a right triangle.
Putting Trigonometry to Work: Solving Missing Sides and Angles
Let’s put our knowledge into practice by exploring various scenarios to find missing sides and angles.
Scenario 1: Finding a Missing Side
Imagine a right triangle with a known angle of 30 degrees and a hypotenuse of 10 units. Let’s find the length of the side opposite the 30-degree angle.
- Identify the known values: Angle = 30 degrees, Hypotenuse = 10 units.
- Determine the trigonometric ratio: Since we’re looking for the opposite side and we know the hypotenuse, we use the sine ratio (SOH).
- Set up the equation: sin(30°) = Opposite / 10.
- Solve for the missing side: Using a calculator or trigonometric tables, we know sin(30°) = 0.5.
0.5 = Opposite / 10
Opposite = 0.5 * 10 = 5 units.
Therefore, the side opposite the 30-degree angle is 5 units long.
Scenario 2: Finding a Missing Angle
Consider a right triangle with a side opposite an unknown angle measuring 8 units and an adjacent side of 6 units. Let’s find the measure of this angle.
- Identify the known values: Opposite side = 8 units, Adjacent side = 6 units.
- Determine the trigonometric ratio: Since we know the opposite and adjacent sides, we use the tangent ratio (TOA).
- Set up the equation: tan(angle) = 8 / 6.
- Solve for the missing angle: Using the inverse tangent function (arctan) on a calculator, we find the angle.
Angle = arctan(8/6) ≈ 53.1 degrees.
Therefore, the unknown angle measures approximately 53.1 degrees.
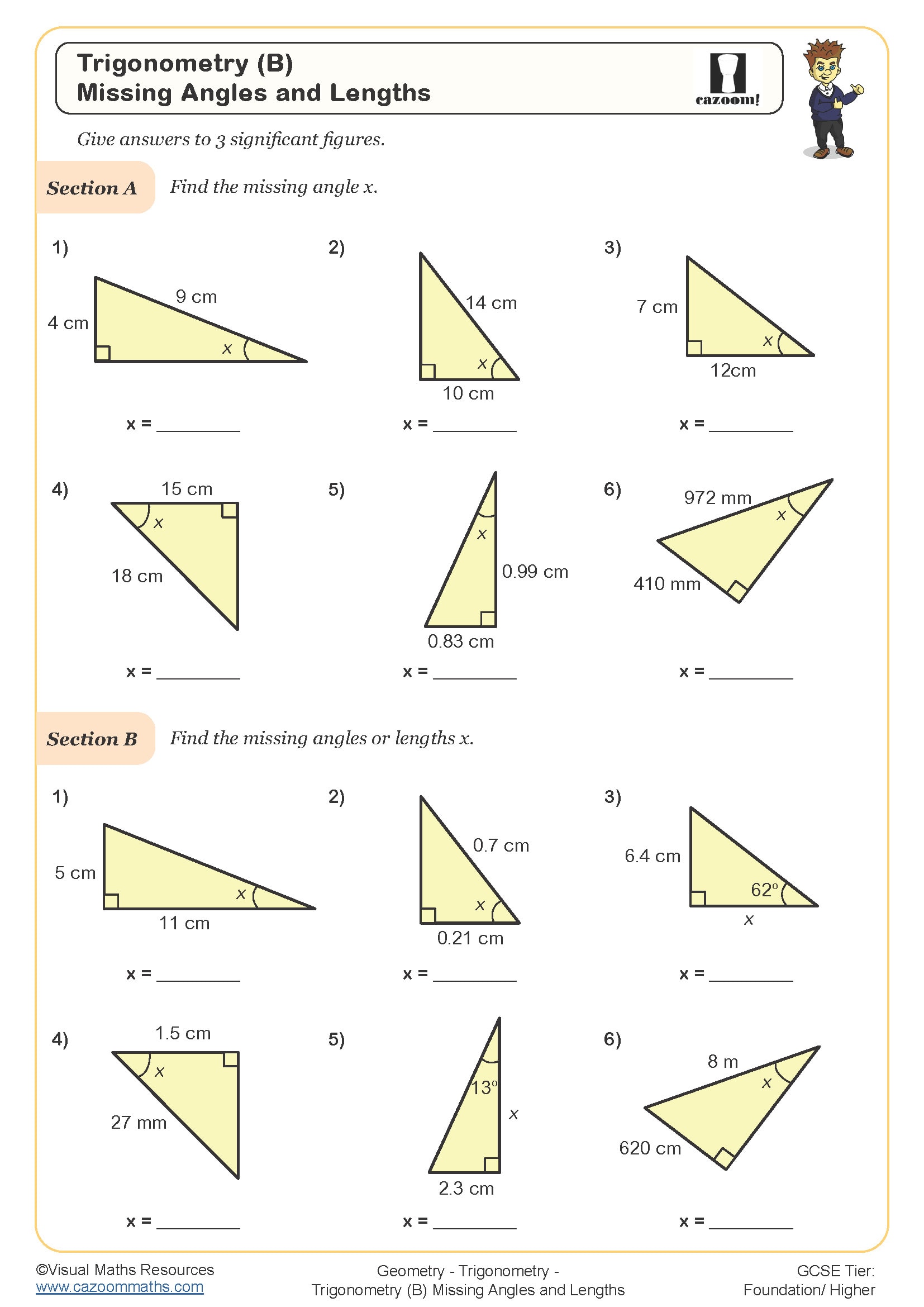
Image: www.cazoommaths.com
Applying Trigonometry to “Real-World” Problems
Trigonometry isn’t limited to theoretical problems on worksheets. It plays a crucial role in solving practical issues in various fields:
- Engineering: Engineers use trigonometry to calculate forces, stresses, and strains in structures, ensuring their stability and safety.
- Architecture: Architects employ trigonometry to design buildings with optimal angles and proportions, considering factors like sunlight and wind resistance.
- Navigation: Navigators rely on trigonometry to determine positions, distances, and bearings using celestial objects and GPS systems.
- Surveying: Surveyors use trigonometry to measure land, construct maps, and establish boundaries.
- Medicine: Medical professionals use trigonometry in radiology and other imaging techniques to analyze and diagnose medical conditions.
Unveiling the Secrets of Trigonometry Worksheets
Now that we’ve explored the fundamentals of trigonometry, let’s conquer those worksheets! Here are some tips to make your journey smoother:
- Remember SOH-CAH-TOA: This mnemonic is your go-to guide for recalling the trigonometric ratios.
- Visualize the triangle: Draw a diagram of the triangle and label the sides and angles. This helps visualize the relationships between the elements.
- Understand the inverse functions: Remember that to find a missing angle, use the inverse trigonometric functions (arcsin, arccos, arctan).
- Practice, practice, practice: The more you exercise your trigonometry skills, the more confident you’ll become in solving problems.
- Seek help when needed: Don’t hesitate to turn to your teacher, tutor, or online resources for assistance if you encounter any difficulties.
Trig Finding Missing Sides And Angles Worksheet Answers
Conclusion: The Power of Understanding Triangles
Trigonometry might seem daunting at first, but by grasping the basic trigonometric ratios and applying a bit of persistence, you’ll unlock a whole new world of problem-solving and real-world applications. So, the next time you face a worksheet with missing sides and angles, remember the principles we’ve discussed here. Approach it with confidence, and unleash your inner trigonometry master! Don’t stop there – explore more advanced concepts and delve deeper into the fascinating world of triangles!





