Have you ever stopped to admire the elegant shape of an ice cream cone or a party hat? These familiar objects are examples of cones, a fundamental geometric shape with a rich history and intriguing properties. Understanding the surface area of a cone is crucial in various disciplines, from engineering and architecture to everyday applications like crafting and packaging. This article delves into the fascinating world of cones, guiding you through the intricacies of calculating their surface area and equipping you with the necessary tools to tackle those surface area cone worksheet answer keys with confidence.

Image: www.pinterest.es
The surface area of a cone refers to the total area covered by the cone’s exterior, including its base and curved surface. To grasp the significance of surface area, imagine yourself trying to paint a cone. The surface area represents the total amount of paint required to cover the entire surface. While calculating the surface area of a cone might sound intimidating at first, with the right approach and understanding, it becomes a straightforward process.
Defining the Components of a Cone
Before we dive into the calculations, let’s define the key components of a cone:
- Radius (r): The distance from the center of the base of the cone to any point on the circumference of the base.
- Height (h): The perpendicular distance from the apex of the cone to the center of the base.
- Slant height (l): The distance from the apex of the cone to any point on the circumference of the base, measured along the surface of the cone.
Decoding the Formula: Unveiling the Surface Area of a Cone
The surface area of a cone is calculated using a simple formula that combines the areas of its base and its curved surface.
Surface Area = πr² + πrl
Where:
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the cone’s base
- l is the slant height of the cone
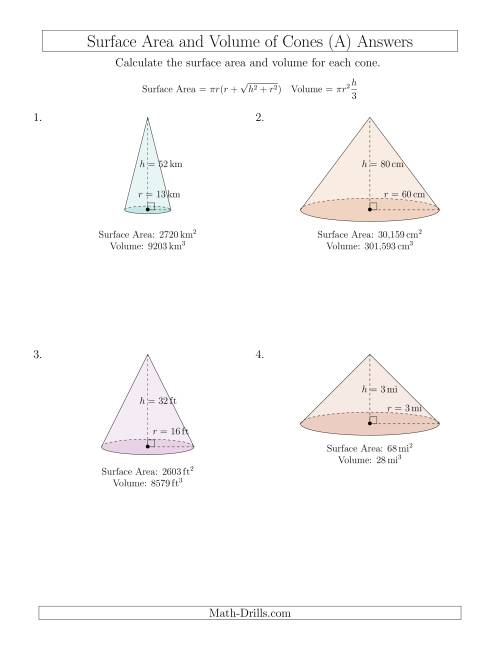
Image: www.math-drills.com
Breaking Down the Formula: The Base and the Curved Surface
The surface area formula consists of two parts:
- πr²: This represents the area of the circular base of the cone. You might recall from your geometry lessons that the area of a circle is calculated by multiplying π by the square of the radius.
- πrl: This represents the area of the curved surface of the cone. Think of the curved surface as a sector of a circle, where the slant height (l) acts as the radius of this sector.
Practical Applications: When Does Surface Area Matter?
The concept of surface area finds practical applications in various fields:
1. Engineering and Manufacturing
- Packaging: Understanding the surface area of a cone allows engineers to design packaging that minimizes material usage and optimizes efficiency. Consider the iconic ice cream cone – its shape maximizes volume while minimizing surface area, leading to cost-effective production.
- Heat Transfer: The surface area of a cone plays a vital role in heat transfer calculations in various applications like heat sinks and cooling systems. A larger surface area enhances heat dissipation, improving the overall efficiency of the system.
- Aerodynamics: In aircraft design, the surface area of various components, including the fuselage and wings, determines their aerodynamic properties. Optimizing the surface area of a cone-shaped wing, for example, can improve lift and reduce drag.
2. Architecture and Design
- Building Design: The surface area of a cone-shaped roof is crucial for calculating the amount of roofing material required and ensuring the stability of the structure.
- Interior Design: Understanding the surface area of a cone-shaped lampshade or a custom-made furniture piece can help you determine the amount of fabric or materials needed for its construction.
3. Everyday Applications
- Party Planning: When designing party hats, understanding the cone’s surface area is essential to calculate the amount of paper needed for crafting. You can also use this knowledge to create unique party decorations that incorporate cones of various sizes and colors.
- Baking and Cooking: Knowing the surface area of a cone-shaped mold allows you to estimate the amount of batter or dough needed for a particular recipe. It helps optimize baking time and ensures consistent results.
Beyond the Formula: Visualizing the Cone
While the formula provides a precise mathematical method to calculate surface area, it’s essential to visualize the cone to comprehend the concept fully.
- Imagine a flat circular piece of paper. Cut out a sector of this circle (a wedge-shaped portion). Now imagine bending the remaining paper so that the two radii of the sector touch, forming a cone. The arc of the sector becomes the curved surface of the cone, and the radius of the sector becomes the slant height.
This visualization helps understand how the curved surface area of the cone is linked to the arc length of the sector.
Example Worksheet: Putting Knowledge into Practice
Let’s consider an example from a surface area cone worksheet to illustrate the application of the formula:
Problem: A cone has a radius of 5 cm and a slant height of 13 cm. Find its surface area.
Solution:
-
Identify the given information: r = 5 cm, l = 13 cm
-
Apply the surface area formula: Surface Area = πr² + πrl
-
Substitute the values: Surface Area = π(5 cm)² + π(5 cm)(13 cm)
-
Calculate: Surface Area = 25π cm² + 65π cm² = 90π cm²
-
Approximate the answer: Surface Area ≈ 90 (3.14159) cm² ≈ 282.74 cm²
Therefore, the surface area of the cone is approximately 282.74 cm².
Mastering the Concepts: Tips for Solving Surface Area Cone Worksheets
To excel in solving surface area cone worksheets, consider these helpful tips:
- Understanding the Formula: Memorizing the formula is the first step. Break it down into its components: the area of the base and the area of the curved surface.
- Visualizing the Cone: Envision the cone in your mind. Identify its components – radius, height, and slant height.
- Using the Pythagorean Theorem: The Pythagorean theorem (a² + b² = c²) helps calculate the slant height (l) when you know the radius (r) and height (h) of the cone.
- Practicing Regularly: Practice various problems from your worksheet and other resources. You can even try creating your own cone problems to test your understanding.
Surface Area Cone Worksheet Answer Key
Conclusion: Empowering Your Understanding of Cones
Cones are much more than just geometric shapes; they are fundamental building blocks for many aspects of our physical world. By mastering the concepts surrounding their surface area, you unlock the ability to analyze and understand various structures and applications. So, the next time you see a cone, remember its fascinating properties and the role it plays in our daily lives. Keep exploring, keep learning, and keep those surface area cone worksheets handy for practice!





