Remember that frustrating moment in high school algebra when you stared at a line on a graph, trying to figure out its steepness? It’s like trying to decipher a cryptic message, right? However, understanding how to find the slope of a line is crucial for numerous mathematical and real-world applications. It’s the key that unlocks a whole world of possibilities! Whether you’re analyzing data, designing a bridge, or simply understanding the rate of change of a situation, the slope of a line becomes a vital tool. In this article, we’ll dive deep into the fascinating world of slopes, equipping you with the necessary skills to master this fundamental concept.

Image: clipartmarlon.blogspot.com
Imagine you’re designing a roller coaster. To create an exhilarating ascent and descent, you need to understand how the slope of the roller coaster track impacts the ride’s thrill. A steeper slope evokes a faster, more heart-pounding experience, while a gentler slope offers a smoother, more relaxed journey. That’s the power of slopes – they reveal the rate of change, guiding you in making informed decisions. Let’s explore the three essential skills to become a slope-master in your own right!
Finding the Slope from Two Points
The most fundamental skill involves finding the slope when you’re given two points on the line. Let’s say you have a line that passes through points (2, 3) and (5, 7). Here’s the formula to calculate the slope:
Slope = (Change in y-coordinates) / (Change in x-coordinates)
To apply this formula:
- Identify the y-coordinates: They are 3 and 7. The change in y-coordinates is 7 – 3 = 4.
- Identify the x-coordinates: They are 2 and 5. The change in x-coordinates is 5 – 2 = 3.
- Divide the change in y-coordinates by the change in x-coordinates: 4 / 3 = 1.33, which is the slope of the line.
Interpreting the Meaning of Slope
It’s not enough to just calculate the slope; understanding its meaning is just as vital. The slope tells us how much the y-value changes for every unit change in the x-value. For instance, a slope of 2 means that the y-value increases by 2 units for every 1 unit increase in the x-value. Think of it as a “rate of change.”
Let’s connect this to real-world examples. If you’re analyzing the sales of a product over time, the slope of the line representing the sales trend indicates the rate of growth or decline. A positive slope points to increasing sales, while a negative slope suggests dwindling sales. The steeper the slope, the faster the rate of change.
Using Slope-Intercept Form
The slope-intercept form of a linear equation is an incredibly useful tool. It provides a concise way to represent a line and directly reveals both its slope and y-intercept. The general equation is: y = mx + c, where:
- m represents the slope of the line.
- c represents the y-intercept, indicating the point where the line crosses the y-axis.
For example, the equation y = 2x + 3 tells us that the slope of the line is 2 (meaning for every 1 unit increase in x, y increases by 2) and the y-intercept is 3 (meaning the line crosses the y-axis at the point (0, 3)). This form makes it super easy to identify the slope and y-intercept, saving you time and effort.
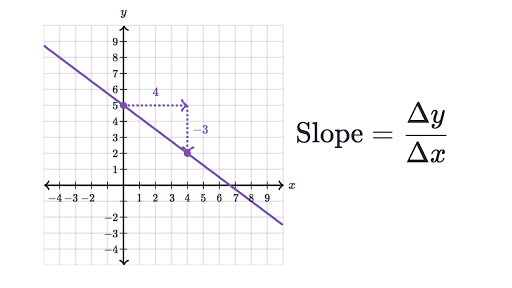
Image: www.khanacademy.org
Latest Trends in Slope Applications
The concept of slopes is not confined to static lines on a graph. It has become a dynamic tool used across various fields, fueled by advancements in technology and data analysis. Here are a few notable trends:
- Machine Learning and Artificial Intelligence: Algorithms leverage slopes to understand patterns and trends within datasets, enabling them to make predictions and make decisions.
- Data Visualization: Sophisticated data visualization tools use slopes to create informative graphs and charts, helping users interpret complex data and gain deeper insights.
- Predictive Analytics: Businesses rely on slopes to model future trends and make informed decisions, impacting areas like marketing campaigns, inventory management, and resource allocation.
Tips for Mastering Slope Skills
Here are a few practical tips to excel in your understanding of slopes:
- Practice, Practice, Practice: Like any skill, mastery of slopes comes from consistent practice. Work through numerous examples to solidify your understanding of formulas and concepts.
- Visualize the Slope: Drawing diagrams and graphs helps you visualize how the slope relates to the change in x and y values. This enhances your intuition and strengthens your comprehension.
- Connect Slope to Real-World Applications: Seek out real-world examples where slopes are used to make connections between mathematical concepts and their practical relevance.
- Explore Different Forms of Linear Equations: Master the slope-intercept form and understand its relationship with other forms of linear equations, such as the point-slope form and standard form.
By consistently practicing these tips and exploring various applications of slopes, you’ll gain a deeper understanding and confidence in your ability to master this fundamental concept.
FAQs
Here are some frequently asked questions about slopes of lines:
- Q: What is the slope of a horizontal line?
A: The slope of a horizontal line is always 0. This is because the y-coordinate remains constant, while the x-coordinate changes. - Q: What is the slope of a vertical line?
A: The slope of a vertical line is undefined. This is because the x-coordinate remains constant while the y-coordinate changes, resulting in a division by zero in the slope formula. - Q: What does a negative slope indicate?
A: A negative slope indicates that the line is decreasing as it moves from left to right. This means that as the x-value increases, the y-value decreases.
3 3 Skills Practice Slopes Of Lines
Conclusion
Mastering the slopes of lines is a crucial step in your mathematical journey. By understanding how to find the slope, interpreting its meaning, and applying it to various real-world scenarios, you’ll gain a valuable skill that will serve you well across numerous disciplines.
Are you interested in learning more about the exciting applications of slopes? Share your thoughts and questions in the comments section below!





